Juros Compostos Equivalentes

Ir para o formulário

1: Conceito

Juros equivalentes faz referência a taxas de juros compostos aplicados em períodos de tempos diferentes. Quando estas taxas de juros (compostos) são aplicadas para um mesmo período de tempo o valor montante (valor final) é o mesmo. Esse é o conceito de Juros Equivalentes.

2: Aplicação prática

O conceito de Juros Equivalentes ajuda comparar taxas de juros diferentes aplicados em períodos distintos, de forma permitir avaliar qual taxa é, de fato, maior e qual é menor. Por exemplo, qual taxa de juros é, de fato maior? Taxa 1: 6,7% ao mês (am) ou Taxa 2: 0,25% ao dia (ad)?

Neste caso a Taxa 1 é menor porque a ela corresponde uma taxa de juros por dia de 0,2164%. Podemos observar que não se trata de somente dividir o valor da taxa de juros mensais por 30 dias. Se assim fosse a taxa 1 de juros seria 0,2233%; o que não é verdade, já que o valor equivalente é 0,2164%.

Isso ocorre porque juros compostos são juros sobre juros; logo, não basta somente dividir a taxa de juros pelo valor. Proceder assim resultará valores errados.

3: Um pouco de teoria

Vamos entender como funciona o cálculo. Se você tem conhecimento elementar de álgebra, então você é capaz de entender todo o cálculo. O primeiro é definir o que é um montante.

Montante é o valor final após um certo período de tempo e é indicado aqui por “M”. Esse valor é fruto de um capital inicial, que indicaremos por “C”. Sobre o valor “C” é aplicada uma taxa de juros que indicaremos por “j”, dentro de um certo tempo que indicaremos por “t”.

A equação que calcula M é:

M = C (1 + j)^t
(equação 1)

Essa é nossa primeira compreensão, definir o valor do montante M. Pelo conceito de Juros Equivalentes, estes são as taxas de juros que quando aplicadas em mesmo período de tempo resulta em um mesmo valor M.

Assim, vamos definir uma taxa de juros 1, e uma taxa de juros 2. A primeira é aplicada diariamente e a segunda é aplicada mensalmente. Nossa busca será como obter uma taxa de juros a partir da outra?

Para isso temos de recorrer aos Juros Equivalentes e seu conceito. Para a taxa 1 temos:

M₁ = C (1 + j₁)^t₁
(equação 2)

E para a taxa 2 temos:

M₂ = C (1 + j₂)^t₂
(equação 3)

Como o conceito de Juros Equivalentes exige que o montante M seja o mesmo, então M = M₁ = M₂; logo:

C (1 + j₁)^t₁ = C (1 + j₂)^t₂
(equação 4)

Como temos “C” dos dois lados da equação, então podemos cancelar, o que resulta:

(1 + j₁)^t₁ = (1 + j₂)^t₂
(equação 5)

A partir da equação 5 vamos isolar uma das taxas, neste caso, escolhemos a taxa 1. Assim, passando o expoente t₁ para o outro lado, temos:

(1 + j₁) = (1 + j₂)^(t₂/t₁)
(equação 6)

Isolando j1, temos:

j₁ = (1 + j₂)^(t₂/t₁) – 1
(equação 7)

Para terminar, multiplicamos por 100 para termos em valores percentuais.

j₁ = 100 [ (1 + j₂)^(t₂/t₁) – 1 ]
(equação 8)

A seguir a equação em um formato de melhor visualização.

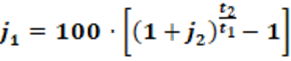
Uma observação importante é que os valores das taxas de juros não devem entrar na equação na forma percentual. Para isso devemos sempre dividir o valor da taxa por 100.

4: Exemplos

Exemplo 1: Vamos começar com o exemplo inicial que apresentamos. Para nosso caso, temos que os juros diários são de 6,7%. Qual a taxa de juros equivalente para o período diário?

Resolução:

Temos:
t₁ = 30 dias
t₂ = 1 mês
j₁ = ?
j₂ = 6,7% = 6,7/100 = 0,067

j₁ = 100 [ (1 + 0,067)^(1/30) – 1 ]
j₁ = 0,2164%

Exemplo 2: Utilizando os dados do exemplo anterior comprove que as taxas de juros são equivalentes através do cálculo do valor montante para cada uma das taxas para um período de 4 meses, para um capital inicial de R$ 100.000,00.

Resolução:

Temos:
t₁ = 120 dias (4 meses)
t₂ = 4 meses
j₁ = 0,2164%
j₂ = 6,7%
M₁ = ?
M₂ = ?
C = R$ 100.000,00

M = C (1 + j)^t : Para a taxa 1, temos M₁ = C (1 + 0,2164/100)¹²⁰ = R$ 129.615,14
M = C (1 + j)^t : Para a taxa 2, temos M₂= C (1 + 6,7/100)⁴ = R$ 129.615,72

Podemos observar que o valor é o mesmo. Logo, as taxas de juros compostos j₁ = 0,2164% ad e j₂ = 6,7% am são equivalentes. A diferença nos centavos é unicamente questão de arredondamento. Caso usemos mais casas após a vírgula, a diferença diminui.

5: Conclusão

Saber calcular as taxas de juros equivalentes são importantes para fins práticos da vida. Pode ser que tenhamos duas propostas diferentes de taxas de juros com aplicação em prazos diferentes. Neste caso podemos comparar os valores fazendo este cálculo.

Ele serve para qualquer caso, para qualquer combinação de prazos e taxas. Além de aprendermos a calcular a taxa de juros equivalente também aprendemos a calcular o valor montante total.