Taxa de Juros Real

Ir para o formulário

1: Conceito

É chamada Taxa de Juros Real aquela que representa a realidade de uma taxa de juros nominal quando a esta é considerada a influência da inflação. O cálculo é feito a partir da equação de Fisher, em homenagem ao economista Irving Fisher (Estados Unidos; 1867-1947).

2: Aplicação prática

Seu uso é fundamental para quem trabalha com aplicações financeiras ou qualquer atividade que envolva taxas de juros. Útil também para saber se um aumento de salário, em termos percentuais, corresponde de fato a um aumento real ou não.

Isso porque a simples aplicação de juros (compostos ou simples) não representa um ganho em si. Para saber se há ganho (ganho real, e não ganho aparente) esse valor deve ser corrigido pela inflação. Ademais, uma taxa de juros nominal de 10%, resultará em valor inferior se corrigido pela inflação.

Nesse caso, uma taxa de juros nominal de 10%, com uma inflação no período de 5%, temos uma taxa de juros real de 4,76%.

3: Soma de valores percentuais

Para entender como isso tudo funciona precisamos fazer um breve estudo. O primeiro a entender é que taxas de juros são valores percentuais. Para somar valores percentuais temos que usar algumas artimanhas. Por exemplo. Acrescente 20% de juros a um produto que custa R$ 100,00.

A forma mais simples de fazer isso é realizar o cálculo em duas etapas.
ETAPA 1: Dividir o percentual (20%) por 100 e este resultado multiplica o valor do produto. Isso resulta em: 20/100 = 0,2; 0,2 x R$ 100,00 = R$ 20,00.
ETAPA 2: Somar o resultado anterior ao valor do produto. Isso resulta em R$ 100,00 + R$ 20,00 =R$ 120,00.

Esse é o resultado final, R$ 120,00. Ainda que esse cálculo seja fácil e simples, existe uma forma mais elegante e igualmente simples de ser feito. Vamos chamar P o valor do produto, no caso, R$ 100,00. Vamos chamar de j a taxa de juros, no caso, 20%.

Se observarmos o cálculo na primeira etapa, temos 0,2 x 100; ou seja; (j/100) x P. Na segunda etapa temos esse resultado mais R$ 100,00; ou seja, (j/100) x P + P. Aplicando um pouco de álgebra podemos colocar P em evidência, que resulta em VALOR FINAL = P(1 + j/100). Aí temos nossa primeira equação. É a equação geral dos juros. Ela calcula o valor final a partir do valor inicial e do juros aplicado. O valor final é conhecido como montante e é, comumente, indicado por M.

M = P(1 + j)
(equação 1)

Na equação “j” não está dividido por 100, mas isso deve ser feito sempre, ou seja, “j” não deve ser utilizado na forma percentual, mas sim dividido por 100.

Tendo isso claro, vamos para o próximo passo do nosso raciocínio. Vamos agora aplicar uma correção sobre o valor M. Vamos acrescentar uma correção de mais 30% e vamos representar esse valor (taxa percentual) por “i”. Vamos indicar esse novo valor final por W.

Usando a mesma lógica, temos W = M (1 + i). Ou seja, nada de novo. Vamos agora expressar isso em termos de “P” e não de “M”. Assim, teremos W = M (1 + i), mas M = P (1 + j); logo, W = P (1 + j)(1 + i).

Disso temos uma importante conclusão: Quando adicionamos 20% sobre o valor do produto, fizemos uma multiplicação entre o valor do produto e (1+j). Quando adicionamos mais 30%, fizemos mais uma multiplicação. Logo, nossa conclusão é: Para somarmos valores percentuais, matematicamente devemos multiplicar os valores percentuais em cadeia.

Quando se fala em multiplicar valores percentuais em cadeia devemos fazer a multiplicação não de “i” ou “j”, mas sim de (1+i) e (1+j). Ou seja 20% + 30%, aplicados sobre um valor qualquer, matematicamente é feito como P x 20% x 30%; ou seja, P (1+20/100)(1+30/100) = P(1+0,2)(1+0,3); ou, em termos gerais, como j = 20% e i = 30%; temos:

M = P(1+j)(1+i)
(equação 2)

Logo, essa é a equação que calcula a soma combinada de valores percentuais sobre um valor qualquer, em nosso caso, P. Caso haja um terceiro ou quarto valor, é só acrescentar os valores percentuais no mesmo formato que aparece na equação 2.

4: Cálculo da Taxa de Juros Real

Feitos esses importantes aclaramentos, podemos seguir em nosso raciocínio. Vamos agora fazer a seguinte análise: A taxa nominal de juros é aquela que vemos em contratos. É a taxa que o banco, a financeira ou a corretora nos apresenta. Vamos indicá-la por n.

Por dedução, a taxa nominal é a soma entre a taxa real e a taxa da inflação. Isso porque na taxa nominal, que é a taxa que vemos nos contratos, dentro dela tem a taxa da inflação e a taxa real, aquela que realmente rende “de verdade”; ou seja:

Taxa Nominal = Taxa Real + Taxa da Inflação
(equação 3)

Isso indica que parte da taxa nominal é para “zerar” a inflação, e o que resta é a taxa real, a que realmente importa para quem aplica os juros. Matematicamente, podemos escrever:

Taxa Nominal = (1 + n) (a)
Taxa Real = (1 + r) (b)
Taxa da Inflação = (1 + i) (c)
(equações 4a, 4b, 4c)

Matematicamente NÃO PODEMOS fazer:

(1 + n) = (1 + r) + (1 + i)

Porque as taxas são valores percentuais e a soma de valores percentuais é feita através da multilicação, lembra??? Então, matematicamente SÓ podemos fazer o que segue:

(1 + n) = (1 + r) (1 + i)
(equação 5)

Agora sim, essa equação tem relevância matemática e é conhecida como Equação de Fisher para a Taxa de Juros Real. Como queremos a taxa real, vamos isolar, primeiramentem, “(1 + r)”.

(1 + r) = (1 + n) / (1 + i)
(equação 6)

Agora vamos isolar “r” e obter, ao fim, a Equação de Fisher.

r = [ (1 + n) / (1 + i) ] -1
(equação 7)

Multiplicamos por 100 para obter o valor percentual.

r = 100 ( [ (1 + n) / (1 + i) ] -1)
(equação 8)

A seguir a mesma equação em melhor formato de visualização.

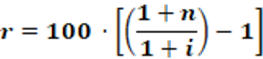
Uma observação importante é que os valores das taxas de juros não devem entrar na equação na forma percentual. Para isso devemos sempre dividir o valor da taxa por 100.

Caso queiramos calcular qual o valor de juros nominais que correspondem a determinado valor de juros reais, temos, a partir da equação 5:

n = [ (1 + r) (1 + i) ] – 1
(equação 9)

Multiplicando por 100 para termos valores percentuais, temos:

n = 100 ([ (1 + r) (1 + i) ] – 1 )
(equação 10)

Por fim, se quisermos calcular a inflação, a partir da equação 5, temos:

i = [ (1 + n) / (1 + r) ] – 1
(equação 11)

Multiplicando por 100 para termos valores percentuais, temos:

i = 100 ( [ (1 + n) / (1 + r) ] – 1 )
(equação 12)

5: Exemplos

Exemplo 1: Vamos começar com o exemplo inicial que apresentamos. Para nosso caso, temos que a taxa de juros nominal é 10%; que a taxa de inflação no período é de 5%. Qual a taxa de juros real para o período?

Resolução:

Temos:
n = 10%
i = 5%
r = ?
Aplicar a equação 8.

r = 100 ( [ (1 + 10/100) / (1 + 5/100) ] -1)
r = 4,76%

Exemplo 2: Vamos agora fazer o cálculo inverso. Vamos calcular qual deve ser o valor da taxa de juros nominal para obter uma taxa de juros real de 10%, em um período com taxa de inflação acumulada de 5%.

Resolução:

Temos:
r = 10%
i = 5%
n = ?
Aplicar a equação 10.

n = 100 (1 + 10/100)(1 + 5/100) – 1 )
n = 15,55%

Essa é a taxa de juros nominal que deve ser aplicada para obter uma taxa de juros real de 10% quando se tem uma inflação acumulada no período de 5%.

Exemplo 3: Por fim, a partir dos valores da taxa de juros nominal de 12% e da taxa de juros real de 8%, determinar a taxa de inflação acumulada no período.

Resolução:

Temos:
n = 12%
r = 8%
i = ?
Aplicar a equação 12.

i = 100 ( [ (1 + 12/100) / (1 + 8/100) ] – 1 )
i = 3,70%

6: Conclusão

Saber calcular os ganhos é importante para evitar surpresas e permitir fazer planejamentos acertados. Considerar a inflação e seus efeitos é necessário para ter uma noção da realidade. Ao não considerar a inflação nosso ganho obtido é mascarado e não condiz com o ganho real.

A equação 8 permite inquirir que se a taxa de juros nominal for menor que a taxa da inflação acumulada no período, o valor da taxa de juros real será, obrigatoriamente, negativa; o que implica que o valor da taxa nominal não foi suficiente para superar os efeitos da inflação.

No caso de a taxa de juros nominal ser maior que a taxa da inflação acumulada no período, a taxa de juros real será positiva, mas menor que o esperado. Para realizar a obtenção do valor desejado da taxa de juros real devemos utilizar a equação 10 que, partindo do valor desejado e tendo conhecimento do valor da taxa de inflação acumulada para o período, podemos calcular a taxa de juros nominal que nos confere o retorno real esperado.